Predicting Transition State Structures with Tensor Field Networks and Transfer Learning

The year 2021 was a Pandora’s Box for machine learning in chemistry. DeepMind put the chemistry world on notice when it published its approach to the protein folding problem [1]. I expect that we will continue to see machine learning approaches quickly dominate the well-defined, data-rich problems in chemistry.
However, there are other challenges that are harder to define, and which require more creativity to leverage limited data.
The Problem
Today we look at TSNet [2], an approach to one of these very difficult problems—the prediction of chemical reaction transition states.
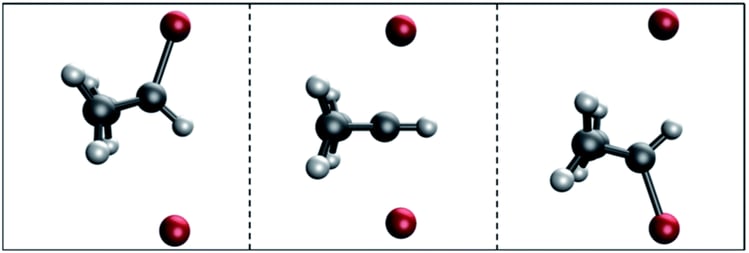
Transition states are intermediate molecular structures: geometric conformations of atoms halfway between reactants and products. Transition states determine the kinetics of a reaction, meaning the reaction rate. Accurate transition state prediction can lead to the ability to design enzymes that maximize reaction rates for arbitrary reactions.
Why is transition state prediction hard? A transition state is a “saddle point” in potential energy space, meaning that it is a potential energy minimum with respect to all physical degrees of freedom, while being the potential energy maximum in one dimension. A transition state is “the maximum energy geometry along the minimum energy pathway between reactant and product complexes”.
Current best transition state prediction methods use a two-stage process:
- Calculating the potential energy surface.
- Hessian-based search – using second-order optimization methods to find the saddle point of that potential energy surface. However, the authors argue that these approaches are sensitive to input quality.
The Approach
The authors’ approach replaces this two-stage pipeline with a single-stage pipeline that predicts the transition state directly from the structures of the products and reactants. Their model architecture is an adaptation of the Tensor Field Network [TFN] that is trained with a Siamese scheme.
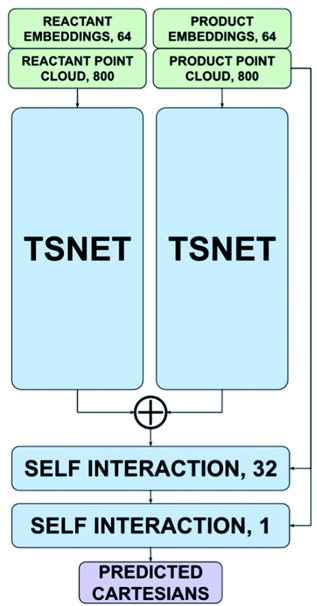
A TFN is a neural network architecture with the unique property of being equivariant – namely, a rotation or translation of the input atom coordinates results in an equivalent rotation/translation of the outputs. This makes it possible to train models that take 3D coordinates as inputs and produce 3D coordinates as outputs.
A Siamese training scheme is one in which two inputs are passed independently through the same model, and then the outputs are combined to produce a loss.
In the case of TSNet, the model takes as inputs the coordinates of the reactants and the coordinates of the products. The reactant coordinates and product coordinates are passed separately through the TFN that represents the “trunk” of the architecture, resulting in two sets of predicted coordinates. The coordinate predictions are then combined by an addition operation to give the predicted transition state.
The authors pre-train their model on the QM9 [3] dataset, then fine-tune the model on a tiny, hand-curated dataset of 53 SN2 reactions. The model achieved a mean absolute error of .3631 Å on the validation set. That may sound decent, but the transition state structures were very similar to the starting reactant and product structures.
Criticisms
The most obvious failing of this approach is the size of the dataset. I know of no world where a deep neural network trained on 53 examples generalizes well. However, I think the authors used the right approach by using an equivariant architecture and sharing weights for the products and reactants by using a Siamese architecture. Given a larger dataset, their model could perform well.
Also, AlphaFold recently had success by using an equivariant architecture recurrently, “cycling” predictions by passing predictions as inputs through the same model. As a result, the model learned physics-inspired protein folding, which generalizes far beyond the training data. I think the authors’ architecture could be improved by using their architecture recurrently, allowing their network to learn physical interactions that generalize better beyond their training set.
Takeaways
What are my main takeaways from this paper? If you are a machine learning chemist, leverage symmetry! Think – what types of symmetry exist in your chemistry prediction task? As another example in this transition state prediction task, there could be multiple optimal transition states that are equally favorable, for example, those which include rotation around a bond of a part of the product distant from the reaction center. These equally optimal structures could be considered part of an “equivalence class”, and a network trained to predict the equivalence class instead of individual instances would likely converge more quickly.
In scenarios with limited data, you can make the most of that limited data by building scientific knowledge into the structure of your neural network.
Sources:
- https://www.nature.com/articles/s41586-021-03819-2
- https://pubs.rsc.org/en/content/articlelanding/2021/sc/d1sc01206a
- http://quantum-machine.org/datasets/
 >
>