Blazing-Fast, High-Accuracy Drug-Protein Docking with EquiBind Geometric Deep Learning

This week we discuss a new paper from the creators and authors of EquiDock [see our related blog on EquiDock that explores “Independent SE[3] Equivariant Models for End-to-End Rigid Docking”].
Today’s discussion relates to EQUIBIND: Geometric Deep Learning for Drug Binding Structure Prediction EquiBind differs from EquiDock in its flexible ligand modeling. Whereas EquiDock performs rigid protein-protein docking, EquiBind allows for ligand flexibility.
In the simplest sense, EquiBind shares the same core algorithm as EquiDock but uses it for drug protein docking. EquiBind predicts the binding location, pose, and orientation of the drug in a single pass, 100 times faster than the next fastest method, and with mean RMSD error of nearly half the error of the next most-accurate method.
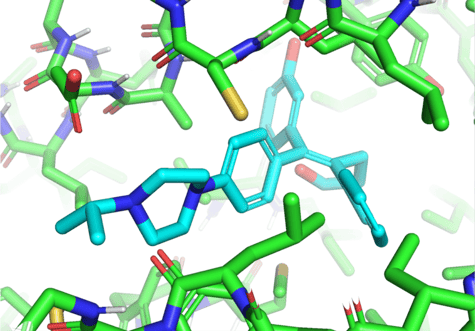
Here’s a recap from our previous blog post about the neural network architecture that EquiBind uses:
- The network takes as input protein coordinates and coordinates of a random ligand conformer [X, X’].
- t constructs a graph and performs equivariant coordinate updates to transform [X, X’] into [Z, Z’], then uses an attention mechanism to predict “keypoints” [Y, Y’] – midpoints between the ligand and protein atoms at the binding site – for both the ligand and the protein.
- The network uses the singular value decomposition [SVD] to find the roto-translation that aligns the two sets of predicted keypoints [Y, Y’] and applies that roto-translation to all ligand coordinates [X’].
- The loss is calculated as the mean-squared error between the predicted ligand coordinates and the true ligand coordinates.
Other terms in this loss are discussed in the previous blog post and the EquiDock paper.
Flexible Ligand Modeling
EquiBind differs from EquiDock in its flexible ligand modeling. Whereas EquiDock performs rigid protein-protein docking, EquiBind allows for ligand flexibility.
The authors offer several possible approaches for modeling this flexibility, but their best approach is to apply a post-prediction correction [C, C’] to match the transformed coordinates [Z, Z’]. They do this in a way that respects physical constraints, namely, preserving bond lengths and angles. To do so, they search for a set of coordinates that maximizes the following formula,
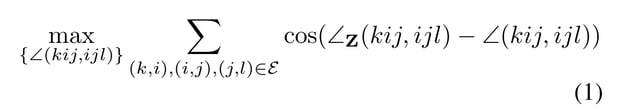
subject to the constraint:
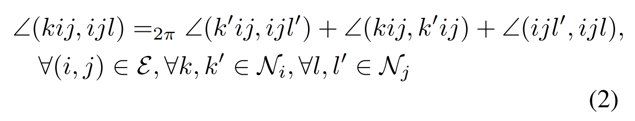
The function to maximize [1] says that it is necessary to find the coordinates that maximize cosine similarity to the transformed coordinates.
The constraint in equation [2] essentially says that, given a change in one torsion angle across a rotatable bond, other torsion angles across that bond will change accordingly. This prevents the maximization of equation [1] while changing bond angles for other atoms around that bond.
This constraint is illustrated in figure 1:
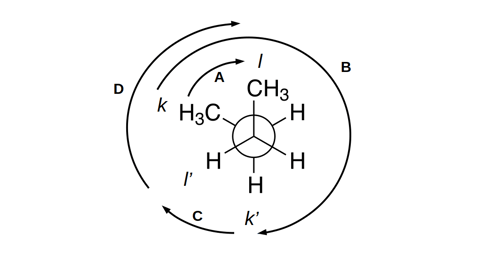 The authors prove a closed-form solution to this maximization problem. This solution is differentiable, allowing for loss to be computed as a function of this “nearest physically plausible conformer to Z”.
The authors prove a closed-form solution to this maximization problem. This solution is differentiable, allowing for loss to be computed as a function of this “nearest physically plausible conformer to Z”.
Superior “Blind” Docking
The results are impressive.
EquiBind is not without limitations. While this model accounts for several known physical constraints of drug-protein docking, it does not account for flexibility of the protein during ligand docking. This is a common, well-known phenomenon in ligand-protein docking; see for example, PDB 1ANF with maltose bound and unbound. EquiBind likely avoids this case because there are known difficulties with modeling protein flexibility about rotatable bonds (the “lever-arm effect“). But accurate drug-protein binding should account for protein deformation. The model also does not explicitly model protein side chains.
 >
> 

