A New State-of-the-Art Model for Molecular Conformer Generation

In structure-based drug discovery, most methods rely on two key elements of accuracy: accurate protein structure modeling and accurate drug structure modeling. AlphaFold is able to predict protein structures with unprecedented accuracy. But drug structure modeling lags behind, with current models for conformer generation only providing 67% accuracy on a common molecular conformer benchmark. GeoDiff predicts drug conformations with a neural network diffusion model, increasing accuracy to 89% on the same benchmark. Improvements in drug modeling cascade to improved prediction of drug affinity, toxicity, and other pharmacokinetic properties, reducing drug development cost and increasing effectiveness and time-to-market.

GeoDiff approaches the problem of predicting the geometric conformation of a molecule from its graph. It builds on a type of generative deep learning model called a “diffusion model”, which transforms a sample from a simple distribution, like a Gaussian distribution, into a sample from a more complicated distribution, like the Boltzmann distribution over molecular conformers. In this post, we will use the example of a conformer and the Boltzmann distribution even when referring to general diffusion models.

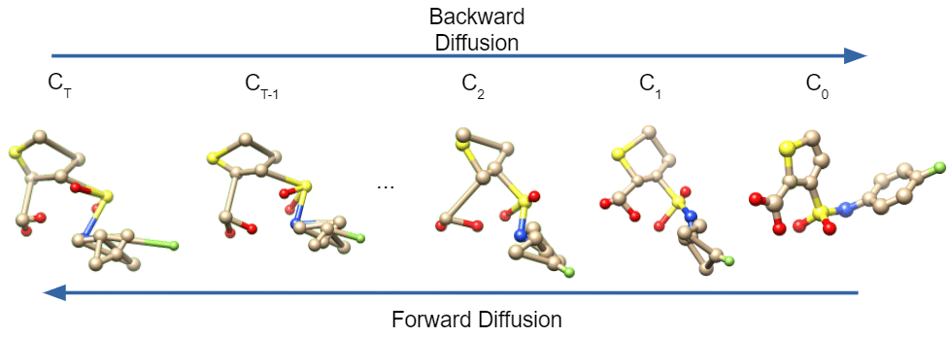
Figure 1:The diffusion process converting a Gaussian sample to a conformer. Forward diffusion goes right to left, backward diffusion goes left to right.

Diffusion models assume a relationship between the Boltzmann distribution and a Gaussian distribution. They assume that, given enough added Gaussian noise, the Boltzmann distribution can be transformed into a Gaussian distribution. This part, which we call the “forward” direction, is easy to model. But diffusion models also presume the existence of a “backward” model that can remove noise from a Gaussian sample to transform it into a sample conformer from the Boltzmann distribution. They treat the process of sampling as a Markov chain of steps, in each step removing noise from a sample from a Gaussian distribution to generate a sample from the Boltzmann distribution.

That noise-removal process must be learned, and is learned by optimizing the “Evidence Lower Bound” (ELBO) popularized by the Variational Autoencoder paper by Kingma and Welling. Essentially, the ELBO is a Kullback–Leibler (KL) divergence loss ensuring that a distribution over latent variables matches a known distribution. In the case of diffusion models, the latent variables are the Markov steps in between a Gaussian sample and the conformer sample. The KL divergence term ensures that, at each step in the Markov chain, the distribution over Gaussian samples with noise removed (backward samples) matches the distribution of conformer samples with noise added (forward samples).

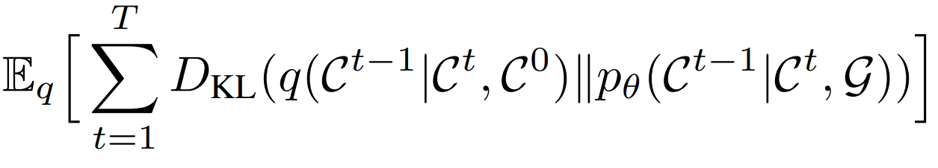
The ELBO objective for GeoDiff. q models backward diffusion, p_θ models (learned) forward diffusion.

This is a very high-level flyover on diffusion models; Lilian Weng has a great blog post deriving the diffusion model objective in more detail.

GeoDiff’s main innovation is a diffusion model designed to be equivariant, allowing it to operate on atom coordinates independent of their original position and orientation.

For its architecture, GeoDiff uses a “Graph Field Network” (GFN) which combines invariant graph features and invariant relative coordinate positions to predict equivariant coordinate updates. This provides equivariance in the backward diffusion process.

However, the forward process of adding Gaussian noise to coordinates is not inherently equivariant. To overcome this, when considering the forward diffusion term during training, GeoDiff centers the coordinates to have zero center-of-mass at each step of the diffusion process and aligns the coordinates with a consistent frame of reference, making the forward diffusion target equivariant.

As far as results, GeoDiff achieves significant improvements (as much as 50%) in the COV-R, MAT-R, COV-P, and MAT-P metrics, which are variants of recall and precision designed to measure how well distributions overlap. For the sake of keeping this post short, I’ll refer you to the paper for a more detailed description of metrics and methods.

This paper will be presented in a few months at ICLR 2022 in the Machine Learning for Drug Discovery Workshop, along with other exciting papers (see our previous posts on EquiDock and EquiBind.