Solving Inverse Problems with Conditional Diffusion Models
What is an inverse problem, and where do inverse problems appear in chemistry?
In deep learning for chemistry, it is common to train a classifier to predict properties of a molecule. But what if you want to generate a molecule with certain properties? There could be many configurations of atoms leading to the same properties. It would be beneficial to be able to sample multiple molecules that are predicted to have those properties. This is called an inverse problem.
The same problem comes up in other chemistry settings. What if you are given a mass spectrogram and asked to find the molecule (or molecules) that produced it? There could be multiple molecules corresponding to the same mass spectrogram, so it would be useful to predict a distribution over molecules corresponding to the mass spectrogram. Any time you have multiple inputs corresponding to a single output, predicting the inputs is an inverse problem.
To put this in math terms, the classification problem is to find p(y|x), where x is the input and y is the label. The inverse problem is to sample from p(x|y). To make this concrete, we’ll talk about an example from a recent paper, Solving Inverse Problems in Medical Imaging with Score-Based Generative Models, by Song et. al.
In this paper, the goal is to reconstruct medical images (CT and MRI) from partial measurements. The images are x, and the measurements are y.
A common approach to solve inverse problems is a “conditional generative model”. The model should be able to sample from the distribution p(x|y). In this paper, the authors use a conditional diffusion model.
A conditional diffusion model is a modification of an unconditional diffusion model. An unconditional diffusion model treats the generation process as a Markov chain of steps that turn data (e.g. images) into noise and vice versa.
 Example of an unconditional diffusion model
Example of an unconditional diffusion model
The forward diffusion process is given by a stochastic differential equation (SDE) which adds noise to the data to convert it into a sample from a Gaussian distribution. The backward diffusion process is a learned SDE, and gradually removes noise to convert a sample from a Gaussian distribution into a sample from the data distribution.
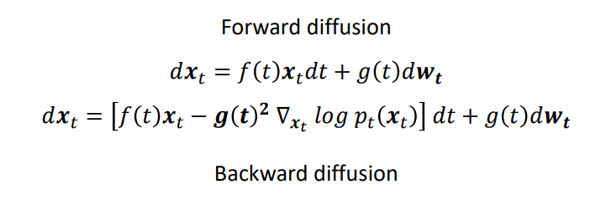 To convert a diffusion model into a conditional diffusion model, the reverse SDE can be conditioned on a value y. In the case of this paper, y is a CT or MRI measurement.
To convert a diffusion model into a conditional diffusion model, the reverse SDE can be conditioned on a value y. In the case of this paper, y is a CT or MRI measurement.
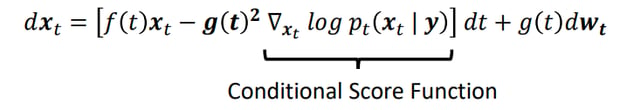
The hard part of this is finding the conditional score function. Other approaches obtain p(x|y) from a classifier trained to predict y from x at each step (called “classifier guidance”) or train the diffusion model to predictp(x|y) directly (“classifier-free guidance”). However, in the case of CT/MRI data, y is a linear transformation of x given by
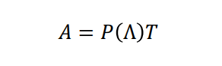 and the best x for a given y can be computed in closed form. This leads to a closed form conditional score function that can be used with an unconditioned diffusion model
and the best x for a given y can be computed in closed form. This leads to a closed form conditional score function that can be used with an unconditioned diffusion model
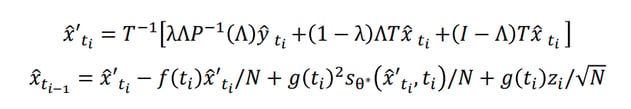
The advantage of this method over other diffusion methods is that it requires no training of an auxiliary classifier p(y|x) and no training of a conditional diffusion model p(x|y) – an unconditional diffusion model p(x) is sufficient. The main limitation is that it only applies to inverse problems for where the output y is a (known) linear transformation of the input x.
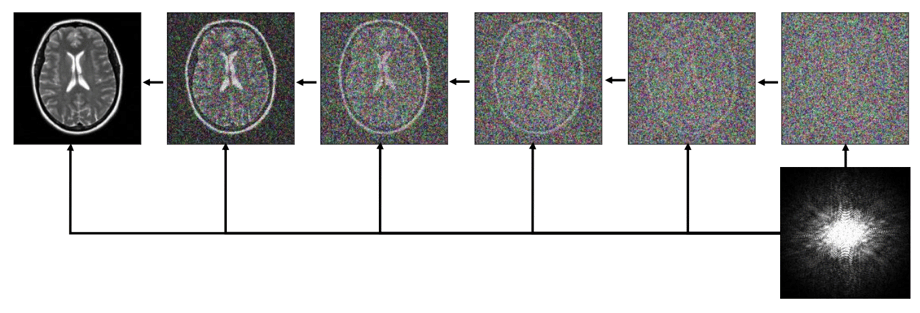 The conditional diffusion model uses the unconditional model without further training.
The conditional diffusion model uses the unconditional model without further training.
The benefit of this method over a simple least-squares reconstruction of x given y is that the reconstruction is conditioned on the prior probability p(x). For underdetermined systems like the transformations given, there is an infinite subspace of least-squares solutions. This method selects the maximum probability image in that space.
The results? With only 10 CT measurements, they achieve comparable accuracy to what the next-best method achieves using 23 measurements. This means that patients experience less exposure to potentially harmful radiation.
Similar techniques can be used for inverse problems in chemistry. Examples include molecule reconstruction from mass spectra, molecular structure determination from electron density maps or electron microscopy data, and any other experiment with multiple possible inputs corresponding to a given measurement.
The conditional diffusion architecture is a promising framework for solving these problems. The use of prior information makes conditional diffusion models a powerful tool for reconstruction problems with limited or noisy measurements.
 >
> 

