Coarse-Grained Molecular Dynamics with Geometric Machine Learning

We live an a world where chemistry computation is increasingly competitive with experimentation. AlphaFold predicts protein structure with accuracy sufficient for many applications. In the limit scenario, computational chemists envision biochemistry simulations on a scale that allows them to trace exact mechanisms of disease. A recent pre-print achieves molecular simulation with nanosecond time steps, which is 1000 times longer than typical molecular dynamics (MD) time steps. It does this while retaining the same macro-molecular behavior as traditional MD. This allows for longer simulations with larger, more complex systems.

Atomic simulations lose accuracy as they increase in computational efficiency. Density Functional Theory (DFT) simulations accurately model bond-breaking and bond-forming at the subatomic scale. Molecular Dynamics (MD) simulations model higher-level inter-atomic interactions via potentials, or force fields, while sacrificing accuracy for bond forming and breaking in exchange for faster computation and longer simulations. The authors’ approach is no different – they trade atom-level simulation for longer simulations that retain macro-molecular behavior.

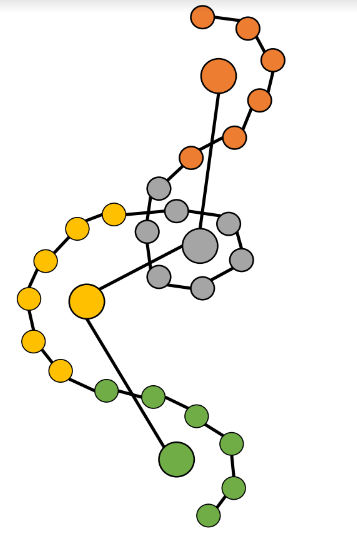
Rather than modeling individual atoms, the approach models cluster centers, called “beads”.

Stochastic Predictions

Because coarse-grained MD leads to inherent approximation error, one goal of the authors’ architecture was to model randomness in the predictions. To do this, instead of predicting a single number for the next time step, the architecture predicts a distribution given by a mean and a variance.

Historical Information

The coarse-graining procedure removes the Markov property of the dynamics, so they also designed their architecture to incorporate historical information from previous states.

Architecture

The model consists of three learned networks which are trained end-to-end.

The first network, the Embedding GNN, takes as input a fine-level (atom-level) graph and produces node embeddings that are shared across time steps. Atoms are then grouped with a graph clustering algorithm.

The second network, the Dynamics GNN, takes as input the node embeddings as well as the node positions and velocities for the last k time steps. Based on their clusters, these embeddings, positions, and velocities are combined into node and edge features for a coarse graph. The Dynamics GNN processes this graph to predict a mean and a standard deviation for the acceleration of the nodes (“beads”) for the coarse graph.

With just the first two networks, the architecture ran into stability issues, experiencing “bead collision”, where two beads come within 1 Å of each other. Thus, the authors added a third “Score GNN” network to predict a gradient of the predicted probability density which, when applied to the predicted coordinates, denoises them to the true coordinates.

The model is trained end-to-end, where the objective function is to minimize the negative-log-likelihood of the data under the predicted distribution.

At inference time, the model predicts bead acceleration, and new bead positions are calculated using Euler integration.

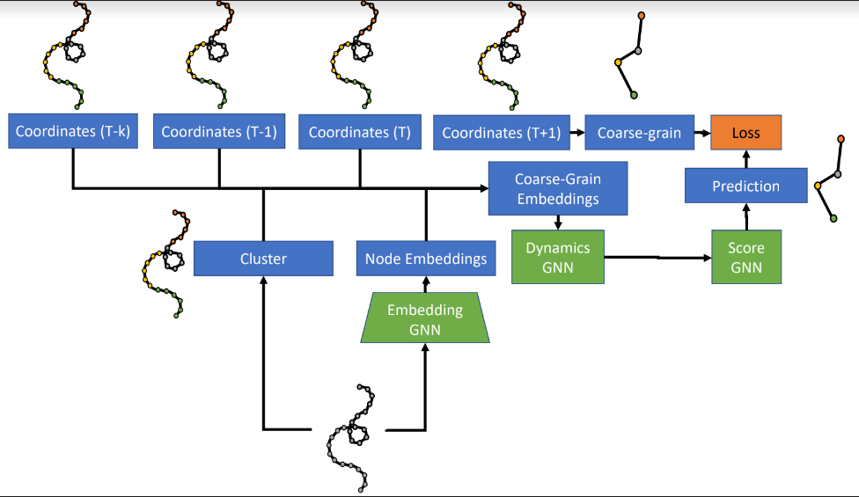
The model architecture.

Results

Because the model does not predict atom-level coordinate updates, they had to find other ways to evaluate their coarse-grained model. One metric is “radius of gyration”, which measures distance from center of rotation. The radius of gyration was found to correlate strongly (r^2 = 0.90) with the true radius of gyration for the coarse states.

The authors also compared predicted and true “relaxation times” of the molecules, and found an r^2 correlation of 0.48. Correlation in this metric demonstrates that the model not only matches the distribution over states, but also captures realistic dynamics.

Conclusion

The authors present a new architecture for coarse-grained molecular dynamics simulation. The model operates on a much larger time step than traditional MD, allowing for larger simulations on larger timescales. This is promising work in the direction of large-scale molecular simulation.

There two main caveats. One is that this network models acceleration of cluster centers, limiting its usefulness for atomistic modeling. However, atom positions can be inferred using techniques like the one described in this paper.

The other caveat is easily remedied, and likely would provide a significant performance boost. The chosen GNN architectures are not equivariant to the frame of reference. Instead they learn equivariance from data, which takes learning capacity away from the task of learning dynamics. This can be easily fixed by using an equivariant architecture for the GNN, for example, an SE(3) transformer.