Bayesian Flow Networks: A Paradigm Shift in Generative Modeling

Generative modeling has undergone a transformative journey in recent times, thanks to the emergence of powerful neural networks. These networks possess an unprecedented ability to capture intricate relationships among diverse variables, revolutionizing our capacity to create coherent models for high-resolution images and complex data. This shift is attributed to the art of decomposing joint distributions into sequential steps, a strategy that surmounts the challenges posed by the “curse of dimensionality.” In this context, a recent preprint (https://arxiv.org/pdf/2308.07037.pdf) by Graves and colleagues at NNAISENSE introduces a game-changing concept: Bayesian Flow Networks (BFNs). This new approach not only delves into the principles of message-passing dynamics but also leverages it for generative modeling, offering unique advantages over conventional methods.
Dynamic Message Exchange: The Core Principle of Bayesian Flow Networks
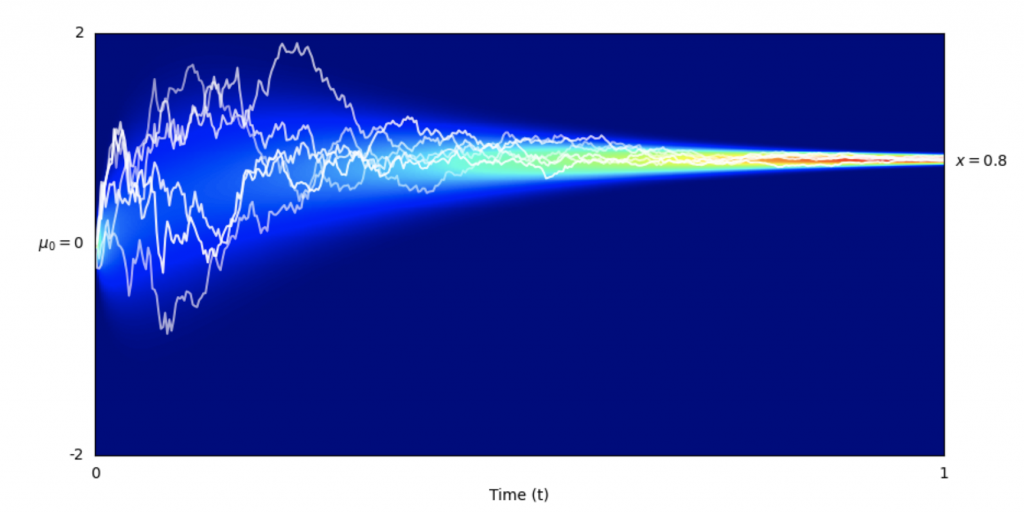
At its core, the concept of Bayesian Flow Networks harnesses the essence of dynamic message exchange. In a metaphorical scenario, Alice imparts insights about data while Bob aims to decipher the message using minimal bits. At each step, Alice reveals more information, and Bob deciphers more efficiently. This paper delves into this iterative mechanism’s application, emphasizing how it forms the foundation of BFNs. These networks distinguish themselves by operating on data distribution parameters, ensuring continuous and differentiable generative processes for both continuous and discrete data. This paradigm represents a seamless integration of Bayesian inference and deep learning, ushering in a new era in generative modeling.
BFNs bear semblance to diffusion models but introduce crucial differentiators. They transition between distributions, not data to distributions, ensuring continuity even for discrete data. This continuity allows direct optimization of negative log-likelihood for discrete data, setting them apart from discrete diffusion models. Furthermore, BFNs hold the advantage of lower input noise levels, initiating from predefined priors rather than pure noise. This unique characteristic accelerates learning on data prone to underfitting. The inherent flexibility of BFNs eliminates the need for forward process definitions, leading to seamless transitions across continuous, discretized, and discrete data, distinguishing them from other models.
These networks introduce a structured framework for data transmission, where information flows through interconnected functions. A sender distribution encodes data into a sender signal, influencing an accuracy parameter. This signal guides the generation of an output distribution, reconstructed into the original data. A receiver distribution accounts for the recipient’s perspective, combining sender and output uncertainties. Bayesian updates adjust parameters based on received information, adapting through an accuracy schedule. The loss function quantifies energy for data transmission, considering discrete steps and continuous processes, making BFNs applicable across various domains.
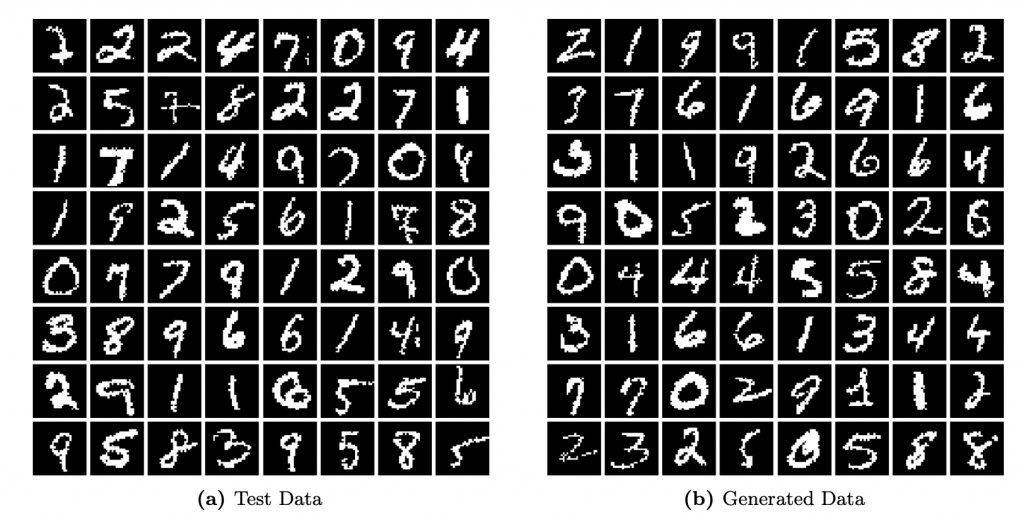
The evaluation of BFNs on diverse benchmarks underscores their potential. From CIFAR-10 images to dynamically binarized MNIST digits and text8 character sequences, BFNs exhibit strong performance. They match or outperform existing methods, showcasing their efficacy across various datasets. In the grand scheme of generative modeling, the introduction of Bayesian Flow Networks marks a pivotal milestone. The seamless integration of Bayesian principles and deep learning techniques brings forth a new tool that redefines how we approach generative modeling, igniting novel perspectives and innovative directions for future research. When working with generative models it’s crucial to have all your information backed up and available for comparison which is why we have developed our life science data hub and LIMS consolidation solutions in order that your data is securely stored and accessible.
 >
> 

